📃Prove schemes and curves
Proof schemes, also known as proof systems or proof protocols, are cryptographic techniques that allow one party (the prover) to convince another party (the verifier) that a certain statement or claim is true without revealing any additional information beyond the truth of the statement. There are several types of proof schemes, each with its own characteristics and use cases.
Since we are utilizing gnark for the creation of cryptographic circuits, it's important to note that it supports two proving schemes: Groth16 and PlonK. These schemes can be implemented using a variety of elliptic curves, including BN254, BLS12-381, BLS12-377, BLS24-315, BW6-633, and BW6-761. To specify the desired proving scheme and the corresponding elliptic curve, an ID is provided within gnark.
Choosing a proving system
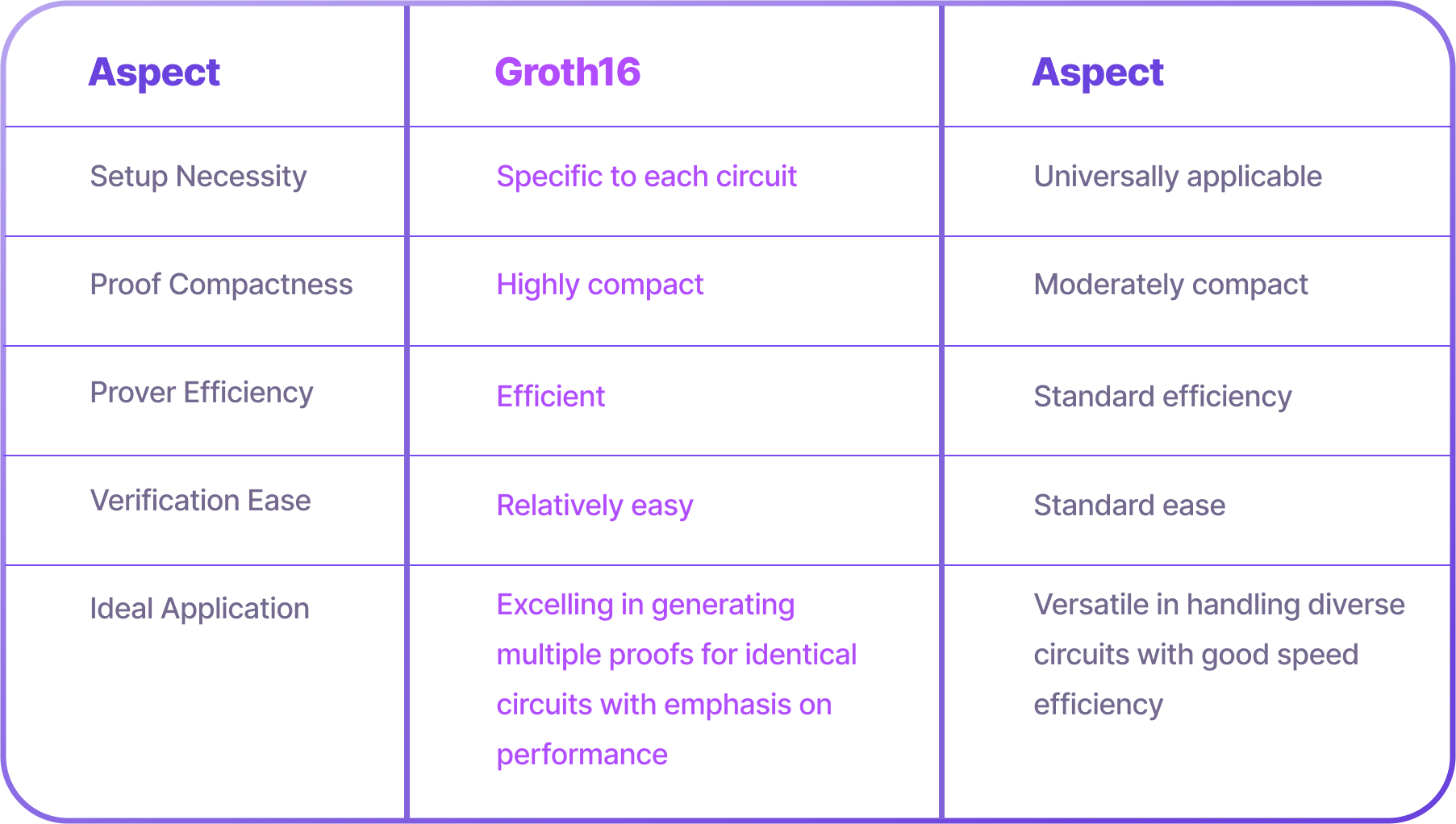
Groth16 : Optimal for situations where the same computational logic is repeatedly proved, making it a go-to for performance-critical applications.
PlonK : A jack-of-all-trades in proving systems, accommodating a broad range of circuits with a balance of speed and efficiency, suitable for varied business logic implementations.
Groth16
Groth16, dating back to 2016, is a pairing-based zk-SNARK widely recognized for ensuring privacy and confidentiality in various applications. Jens Groth described it as a succinct proof system that efficiently verifies complex algebraic relations using elliptic curves' bilinear pairing properties. This protocol is particularly adept at proving knowledge of a witness (a set of field elements satisfying a polynomial equation) about a statement, leveraging algebraic relationships and computations in elliptic curve groups.
Key Characteristics:
Zero-Knowledge Property: Enables a prover to affirm the truthfulness of a statement without divulging underlying data, meeting completeness and soundness requirements.
Succinct Proofs: Proofs in Groth16 are short and concise, containing only three group elements. This compactness is vital for applications like blockchain systems, where proof size is a constraint.
Protocol Steps: The Groth16 protocol involves setup, proving, and verification phases. The setup phase is crucial, requiring a secure and trustworthy ceremony to prevent potential attacks or backdoors. The proving phase involves constructing a succinct proof, while the verification phase is about checking the proof's validity without gaining additional information.
Applications:
Groth16 has been adopted in various domains, such as anonymous credentials, privacy-preserving cryptocurrencies, and decentralized finance (DeFi), where preserving privacy and proving correctness are essential
PlonK
PLONK, introduced by Ariel Gabizon, Zac Williamson, and Oana Ciobotaru, is a general-purpose zk-SNARK scheme that has gained attention for its efficiency. It builds upon prior zero-knowledge proof protocols like SONIC and Marlin, introducing improvements for enhanced usability and efficiency.
Key Characteristics:
Universal and Updateable Trusted Setup: PLONK's trusted setup is both universal and updateable, allowing use across various programs and enhancing security through a multi-party sequential procedure.
Polynomial Commitments: Utilizes "Kate commitments," a type of polynomial commitment for verifying polynomial equations. PLONK's flexibility allows the use of alternative schemes like FRI or DARK, accommodating various use cases and developer preferences.
Efficiency: PLONK reduces the computational burden on the prover, requiring fewer polynomial commitments and opening proofs, thereby improving efficiency and scalability in practical applications.
Applications:
PLONK's design, which minimizes the prover's workload and offers a more compact Structured Reference String (SRS), is well-suited for applications where efficient computation and reduced storage are crucial
Why we are using Groth16
Performance Efficiency: In blockchain applications, especially those involving frequent transactions or operations that require repeated proving of the same computational logic, performance is key. Groth16 is highly efficient in scenarios where the same circuit needs to be proven multiple times, which is often the case in blockchain networks. This efficiency is crucial for maintaining fast transaction times and lower computational costs.
Succinct Proofs: The proofs generated by Groth16 are notably short and concise, comprising only three group elements. This is particularly beneficial for blockchain systems where minimizing the size of proofs can lead to significant reductions in storage requirements and network bandwidth, enhancing overall system scalability.
Zero-Knowledge Property: Groth16 provides strong zero-knowledge guarantees, allowing the prover to validate the truth of a statement without revealing any underlying data. This is essential in blockchain applications where privacy and confidentiality are paramount, such as in the case of private transactions or confidential contracts.
Security and Soundness: The cryptographic strength of Groth16, which relies on the hardness of problems on elliptic curves, ensures a high degree of security. This aligns with the need for robust security in blockchain applications, where the integrity and trustworthiness of transactions are critical.
Mature Ecosystem and Integration: Given the widespread use and maturity of Groth16 in various blockchain platforms, there's a robust ecosystem of tools and libraries available. This can facilitate easier integration and implementation in your blockchain projects, especially considering your expertise in Golang and JavaScript, as tools supporting these languages are likely available.
Compatibility with Ethereum and Other Platforms: Since you're working on a rollup-as-a-service platform, compatibility with major blockchains like Ethereum is crucial. Groth16 is compatible with Ethereum 1.x (using BN254 curve), making it a suitable choice for applications targeting Ethereum-based rollups or similar environments.
Choosing an elliptic curve
Both Groth16 and PlonK (with KZG scheme) need to be instantiated with an elliptic curve. And we use gnark in our system and since gnark supports six elliptic curves: BN254, BLS12-381, BLS12-377, BW6-761, BLS24-315, and BW6-633. All these curves are defined over a finite field and have an equation of the form
To effectively work with Groth16 and PlonK cryptographic protocols, it's crucial to select the right elliptic curves. These curves must meet several key requirements:
Security: Ensures the soundness of proofs.
Pairing-Friendly: Vital for proof verification.
Highly 2-Adic Subgroup Order: Enhances efficiency in proof generation.
Specific Curves and Their Use-Cases:
BN254: Used in Ethereum 1.x. This curve is the only one supported currently, with other curves proposed in EIPs (EIP-2539, EIP-2537, EIP-3026) but not yet integrated.
BLS12-381: Utilized in Ethereum 2.0, ZCash Sapling, Algorand, Dfinity, Chia, and Filecoin. It's recommended for platform-agnostic applications due to its balance of security and practical speed, though it's slower than BN254.
BLS12-377 and BW6-761: Ideal for applications requiring one-layer proof composition (proof of proofs). These curves are secure, pairing-friendly, and have a highly 2-adic subgroup order. BW6-761’s subgroup order matches BLS12-377's field characteristic, which is essential for efficient proof composition. They are used in ZEXE, Celo, Aleo, and Zecale.
Trade-offs and Recommendations:
For Ethereum 1.x applications, BN254 is the go-to curve.
For Ethereum 2.0 and broader applications, BLS12-381 is advisable for its enhanced security.
For one-layer proof composition, BLS12-377 and BW6-761 are the best choices.
Specialized Curves - BLS24-315 and BW6-633:
In Groth16, operations occur in three groups (G1, G2, GT), but in PlonK (with KZG), they occur in G1 and GT only.
BLS24-315 is optimized for G1 and competitively for GT. Paired with BW6-633 in a 2-chain setting, it facilitates efficient PlonK one-layer proof composition.
This pair is secure, pairing-friendly, optimized for KZG-based SNARKs (like PlonK), and has a highly 2-adic subgroup order. BW6-633's subgroup order equals BLS24-315's field characteristic, crucial for efficient proof composition.
In summary, the choice of elliptic curves depends on the specific requirements of your blockchain application, balancing between security, efficiency, and the type of cryptographic proof system used.
Why we choose BLS12-381
Security: BLS12-381 is known for its strong cryptographic security. It's designed to provide a high level of security against potential cryptographic attacks, which is crucial in blockchain applications where the integrity and trustworthiness of transactions and contracts are paramount. Its security level is in line with current cryptographic standards, making it a robust choice for safeguarding blockchain transactions.
Pairing-Friendly Nature: One of the critical requirements for elliptic curves used in zk-SNARKs like Groth16 and PlonK is being pairing-friendly. BLS12-381 meets this requirement, facilitating efficient proof verification. This property is essential for implementing zk-SNARKs, as it allows for the creation of compact and efficient cryptographic proofs.
Adoption in Major Blockchain Platforms: BLS12-381 is utilized in several prominent blockchain platforms, including Ethereum 2.0, ZCash Sapling, and others. This widespread adoption means there's a significant amount of research, development, and real-world testing backing this curve. By choosing BLS12-381, you are aligning with an industry standard, which can be beneficial for interoperability and future-proofing your applications.
Balance of Security and Speed: While BLS12-381 may not be the fastest curve compared to others like BN254, it strikes a balance between security and practical speed. In blockchain applications, this balance is crucial as it ensures that while transactions and operations are secure, they also occur at a reasonable pace, which is essential for user experience and scalability.
Platform-Agnostic Nature: BLS12-381 is recommended for platform-agnostic applications, which is particularly relevant for a rollup-as-a-service platform like AirChains. Since you might be catering to a wide range of clients with diverse needs and blockchain bases, using a curve that is widely accepted and used across different platforms ensures greater compatibility and flexibility.
Community and Tooling Support: Given the popularity of BLS12-381 in the blockchain community, there's a rich ecosystem of tools, libraries, and community knowledge. This can be advantageous for development and troubleshooting, especially considering your expertise in Golang and JavaScript.
Future-Proofing: The ongoing evolution of blockchain technology and cryptographic standards suggests that choosing a curve with a strong track record and broad adoption, like BLS12-381, positions your projects well for future developments and standards.
Last updated
